E.K. Wolff

Institute for Applied Biotechnology and System Analysis at University of Witten/Herdecke, Stockumer Str.10, 58453 Witten, Germany

^*Corresponding Author: E.K. Wolff, Institute for Applied Biotechnology and System Analysis at University of Witten/Herdecke, Stockumer Str.10, 58453 Witten, Germany

Received: 07 April 2025; Accepted: 14 April 2025; Published: 20 May 2025.

Article Information

Citation: E.K. Wolff. Contextual System-Theory. Journal of Analytical Techniques and Research 7 (2025): 23-29.

DOI: 10.26502/jatr.48

Abstract

Keywords

System-analysis, Complex systems, System-theory, Biological systems, Object oriented programming, Artificial intelligence.

Article Details

1. Introduction

For more than hundred years we have lived in an age of science. Natural science and technology have determined our thinking and daily activities. Looking for causal dependencies is the basis of our arguments in any discussion. What we are not aware of is, that all causality we argue with is based on models. Even though these models are very often derived by a good reliable database, none of these models can be really verified. They may have a high plausibility and thought to be "true", but if one looks closer into it, the “reality” is much more complex. G. Nicolas and I. Prigogine wrote at the beginning of their book [1] “Exploring Complexity”: "Our physical world... is a world of instabilities and fluctuations, which are ultimately responsible for the amazing variety and richness of the forms and structures we see in nature around us. New concepts are clearly necessary to describe nature, in which evolution and pluralism become the key words."

For almost the same hundred years, scientists debate about causality. In the beginning of the nineteenth century paradigm changes were introduced. It all started with nuclear disintegration and quantum-mechanics. Only introducing statistical behavior into the new types of models fulfilled the non-causal descriptions of the observed phenomena. In addition, Heisenberg showed with his uncertainty principle [2] that even two dimensions of a System cannot both be exact, so distribution-functions were introduced. All the models we use are simplified for our limited human view. We never learned complex thinking in school or even in university. Part of this is due to our evolution. In extreme situations (for our early ancestors: Human - Lion Situation) we have to be able to make fast decisions. So our brain developed to simplify and minimize, to decide fast and linear. In an evolutionary sense, we are in a Stone Age state and cannot keep up with the technical and scientific revolutions of the science century, but our own environment has changed to be much higher in complexity. Globalization and environmental problems form world networks of interdependencies, which cannot be described with simple system models. Even in modern science one starts with a simple model to explain an isolated case of a complex system. Then gradually the model is built up step by step to a more complex situation. This approach I call inside-out modeling. It works fine in low complexity and ideal model situation, but to describe high complex systems, one needs a paradigm change turning the procedure upside down. In the following chapters the basis of a "Contextual System-Theory" for modeling complexity as an outside-in procedure will be developed.

2. Methods and Definition

The whole is the whole, it includes everything. All that exists; all that was thought or can be thought of; all laws and their contraries; meaningful or meaningless and much more;

all that one can imagine or never be able to. Just,

                                                                                    All

If one turns the classical procedure upside down, one has to start with the whole, the whole world or everything. This will be called the

All-System or shortly                                             A

The

exists of all

All-System A

elements e

which are                                                                  existent

An element e is existent, if it is

                                                                     experienceable (experimenting) ε

by itself

                                                                     Self-experienceable iε

                                                                     intrinsic-existent or self-existent

or by another element e

                                                                     extrinsic-experienceable eε

                                                                     extrinsic-existent

Describeable d (describing) means, the experiencable element e becomes a

                       structure s

Communication c

is the transfer of a structure s to an (other) element e

Let me pause for a moment before continuing with the definition part and discuss some consequences. Thinking for example is a sub form of describing d so it forms in self- communication c with the element eb (brain) a new structure sb in itself, if one locate thinking to the brain.

Another consequence is, c effects our communication language. Languages Sl are Systems, which have a structure sl, determined essentially by its grammar εl and its syntax σl.

Time, Sets, Context and Operation

The All-System A include the element et, short t the Time (even if one include the relativity theory of Einstein, one would need to take the space-time into account). Only a system including the Time t, can be closed. It is self-evident, that the All-System A is closed.

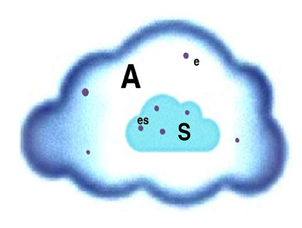
Parts of the All-System A can be divided into

                                                                                   Subsystems S

which consist of the              

                                                                                   elements es

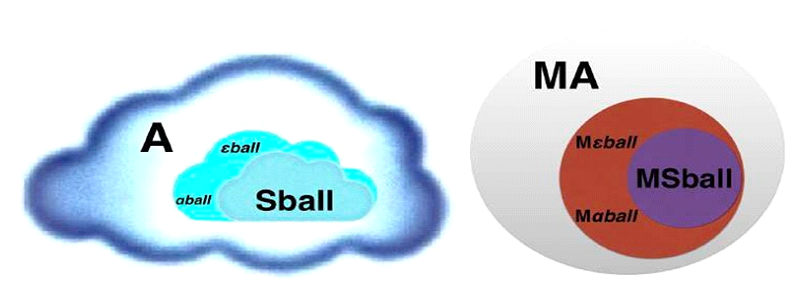
represented symbolic in the descriptive graph of figure 1.

Figure 1: Descriptive graphic representation of the All-System A and the subsystem S with their elements e and es

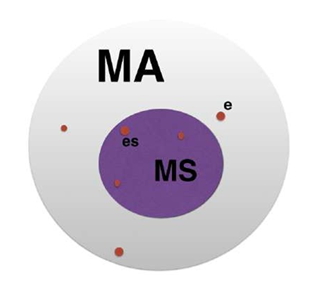
To each of the above and further described - defined instances - exist an associated set M. For example MA or MS are the associated sets of the All-System A and Subsystems S respectively as displayed in figure 2.

This step reflects two representations of systems. The first one is the descriptive and more general holistic one, which is open, "formless" and does not have to have rules, although it can. The second one is the formal one with defined rules and structures.

While introducing the formalism of sets, one already mathematize and starts to model using mathematical rules and a mathematical language. As it will be shown later, sometimes one even has to find new formalisms to expand the classical mathematical language, fulfilling necessities for describing phenomenons, which cannot be handled with classical mathematics.

Figure 2: Formal graphic picture of the sets MA and MS with their elements e and es

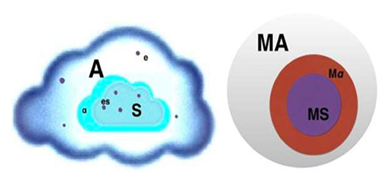
All Subsystems S as well as all elements e are connected by interactions actions α

It follows directly, that actions α are part of the experienceable (experimenting) ε (consequently communication c is an action). For more clarity we will call all experienceable actions with the elements e as ε giving e a structure s while α describe more the interaction between two or more elements (figure 3). It can also form structures in elements. (For example: a ball reflects in the interaction with a white light source red light and is noticed by our eyes as a red ball. But if the light source is pure green, the ball is black for our eyes. Is it now black or green?).

Figure 3: Descriptive (left) and formal (right) representation of the interactions to the allsystem

Everything has a context. Complex systems especially have to be viewed in connection to their contexts. One tend to simplify this aspect and forget the complexity of the interactions to other systems and its surroundings. The most mistakes one easily makes, is to presume the reproducibility of the contextual situation. One always has to obey the time dependence of the context in modeling complexity. Developing a new system theory it is necessary to include the context.

The

                                                                                          Context KS

Is a Subsystem which includes the Subsystems S and all actions αs from Subsystems S with the rest of the All-System A.

So all

                                                                                          actions αs are KS-S.

The same should be true for all associated sets M.

As important as obeying the contexts of systems, is to look differently to our understanding of time dependency. All system-elements e are time dependent as well as their actions αt.

What is usually called constant is never time independent. One could formulate it possibly the way, that αt is a process, with no measurable change in times of single “infinity”. (What ever “infinity” means, it has to be defined for every case).

                                                                                          αt(0)~ αt(t) and αt(t) ~ αt(t+∝)

A Subsystem S can be self-identical, but two Subsystems S1 and S2 can practically never be equal, because of the high context sensitivity KS, statistical elements esst part of the set of es and its time dependence est. Therefore, let's introduce:

                                                                                          proximity εp

Similar Subsystems S form in the n-dimensional System-space cluster which have a proximity εp, where all Subsystems S have the

                                                                                          Distances ed

from each other.

The Distances ed themselves are elements of the associated Subsystems S or structures of its elements. So the proximity εp describes the distribution of the Distances ed in the cluster. Instead of talking about “equality” we should think about “similarity”. In the place of "comparable" we put "categorization" - that means: to order in Distances ed, the relative closeness in the n-dimensional system space. The categories have no fix borders like drawers, they form open like clusters. These differ from other clusters in their different probabilistic centers.

It is a basic principle of complex systems that they can be contextualized. Because of the statistical part of the system parameters and elements, the context will be variable and fluctuate in time.

So the stability of a system is always a function of time, and it depends on the elasticity and therefore on the adjacent contextual laws of the System. All systems are time unstable or better “quasi stable”, only the spaces (system owned period) of time are different, depending on the context. The natural laws, part of our mathematical view to the world, belong to this context.

The characteristic space of time of special systems vary a lot, even in similar system- domains. For example in living systems the space of time-domain starts with ms (e.g. flies etc.) and ends with several thousand years (e.g. trees, funguses etc.). The time-domain of lifeless material reaches from atoseconds or smaller to the existence of the universe (e.g. elementary particle systems, quantum mechanical systems, geological systems, astronomical systems etc.).

One consequence of this part of complexity is the deterministic chaos of systems such as, the butterfly effect, which E.N. Lorenz described [3,4] for the first time, that weather is influenced by the beat of a butterfly’s wing even far away from us. One does not have to look for such high complexity like meteorological systems to find deterministic chaos, already the three - body system is unpredictable in its time course and forms a deterministic chaotic system.

The second consequence of complexity, due to the Heisenberg uncertainty principle, follows as the fuzziness of complex systems. A similar effect will arise from indeterminable fluctuations like statistical noise. So it is essential to include these aspects into the system’s description or modeling. In logic type of modeling, you could use fuzzy-sets, while in the mathematization of complex systems one needs statistic-operators like in quantum mechanics. All these effects will be discussed further in a later publication of this series as well as the symbolic visualization of complex systems like Feynman [5] visualized in his graphs the complexity of quantum interaction in elementary particle physics. This kind of graphical approach could be developed for complex systems as well.

The

                                                                                          Operation Ω

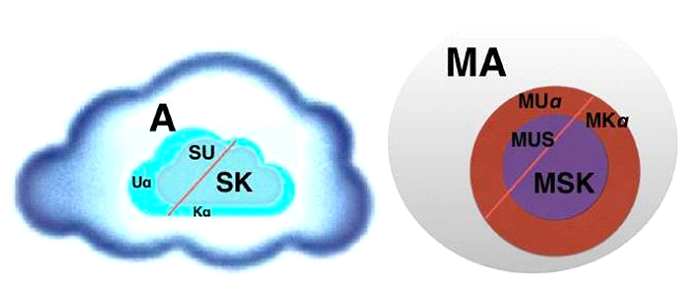
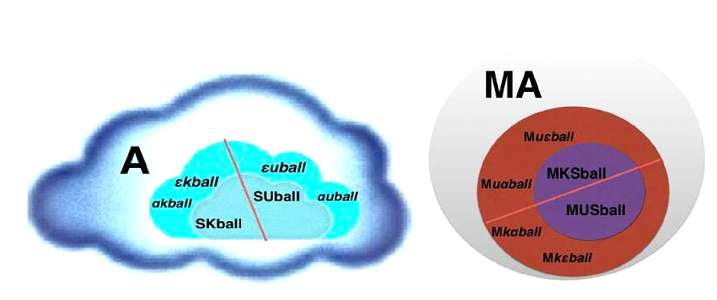
is an amount named classes of actions αs to do experiments for describing Subsystems S. This can be a personal subjective Interpretation ιs, or a more objective Analysis σs by a measuring system like in analytical methods (Spectroscopy, NMR, ESR, AFM, Electro Microscopy etc.). Neither of these are ever complete, because the subject can never sense all possible properties of S, nor are all known apparatus or measuring systems able to do it. So the described Subsystems S falls into two parts, Subsystems SK the known one and Subsystems SU the unknown (figure 4).

Figure 4: Graphic demonstration of cutting (descriptive (left) and formal (right))

Another operation, processes of analysis, we have to define, I call cutting. This is the process of analyzing the Subsystem and categorizing the Subsystem with its interactions α due to the All-system A. Or another subsystem S0, which includes the subsystem S totally or partially. This way we define the borders of the Subsystem due to it’s surrounding in the n- dimensional space.

The cut C defines the borders of the subsystems to its surroundings of S0 or the space of the All-system or both. It can be inclusive "Ci", so all objects lay inside of the Subsystem S and are Elements of it, or exclusive "Ce", where all Elements are outside and not objects of S. A mixture is possible. In this case the cut Cie has to be defined for each dimension or classes of dimensions of its n-dimensional system-space separately. Very often one can approximate it by a distribution function.

At this stage the defining part gave all necessary definitions so far and we can start to practice describing real systems.

3. Results

From here on, part of the "modus operandum" of modeling complex systems will be described. Later articles will go deeper into the whole process of contextual system-analysis and its steps. First I formulate the classical way of going "inside-out", following turning this around going "outside-in”. Let's start with a putative simple system, a ball.

A Ball

Lets throw a small, heavy ball and describe its three demential way in time. Classically we would use Newton's laws of universal gravitation and get pretty good results. If we take a larger ball, which is even lighter, we have to add aerodynamic resistance and in case of upcoming wind the situation becomes quite complicated. But still we just take the basics of

Newton's laws and combine it with other classical physical principles. If the situation is normal, which means average, everyday conditions, we get for the most part (excluding extreme cases) good, practical approximations. Even if the use of other more complex mathematical descriptions would not fulfill our needs. We normally solve all these problems via numerical approximation, irrespective of the concrete conditions, like having water instead of air or other media such as a beach ball instead of a small heavy one and so on. We can simulate almost all usual circumstances precisely enough with modern numerical techniques. What will fall by the wayside using this approach, is the deeper understanding of the underlying dependencies. As a soccer fan, I would like to know how to curl the ball from 20m away directly into the top right corner of the goal. The special outer surface, as well as the spin and inner inhomogeneous fluctuations of the ball, are partially responsible for the movement. As far as I know, no one has yet found a reasonable way to explain this. Only the striker himself, with intensive training, can learn to kick the ball, with good probability, into the top corner.

The process, starting with a simple model and refining it by adding more complexity, will obstruct the view to the whole. Let me therefore at this point change to the outside-in procedure.

We start with the All-System A wherein our ball SBall is a subsystem, which does not contain only the balls, I was talking about, but all the balls one can think of and even the ones we cannot imagine. As kids we used a can or crumpled sheet of paper to play soccer, this was our ball. In rugby or American football the form is more of an egg-like structure than a sphere. All of this, color, material and so on are experiences with the ball and are described by εball the interactions we summarize in αball. The following figure 5 shows this situation in the general descriptive (left) or more mathematical form (right).

Figure 5: Principal representation (descriptive (left) and formal (right)) before brainstorming

The next step is brainstorming about all what we understand about balls, their properties as well as all interactions between the balls and with their surroundings. This is one of the most important steps in the whole analysis and it has to be done thoroughly without missing any developments in the field of balls and the associated ones. This step has to be fulfilled all the time iteratively to be as complete as possible.

After this we set the cuts, which is just as important and also needs conclusive brainstorming to determine which are not balls. It will give us the borders to the All-System A and the associated Subsystems S. So we get the following situation, shown in the next schemes (figure 6).

Figure 6: Principal representation (descriptive (left) and formal (right)) including the unknown

Why do I make a ball so complicated? First of all it is a simple example to demonstrate the principles of the outside-in system-analysis. Secondly, if I include a satellite being part of balls, it becomes even clearer for such a simple example, as a ball. Suddenly, if the satellite flies for several ten years in space to reach the far astronomical objects of our solar system, the space-time, the space-curvature, quantum-relativity etc. has to be included and the ball becomes a much more complex system. So the model of our ball is highly dependent how looking at it.

The surrounding, its objects and their interactions with the subsystem Sball I call the Context Kball. The Context K of a Subsystem S summarizes all experienceable ε and with it all actions α between the outer elements of S. The graphic representation of inner elements will be discussed in the next article in details.

Let's come back to earth, there is enough complexity here in our daily life.

A Forest

A Forest is a highly complex system, which forms its own biocoenosis. A lot of subsystems are working together. Not only that, this biocoenosis is not understood, this is true for almost all its subsystems and even the trees themselves. As an exception we will in this case start with the cut, because we define, for ease, the subsystem forest, SForest as an area of trees. This means, where the trees end is the border of what we call a forest. But where do they end? This is not so easy to decide. For that the mean distance εdm of the trees has to be defined to know when an area is a forest. The distance εd is an operator, which describes in the mathematical approximation the density-function in the forest area. If we take the distribution function as the measure for defining the forest we define the border as 5 times the mean of εd. Each tree, which lies on its own outside is not part of the forest. (In practice it is much more complicated as described here - were starts the savanna, were ends the forest? - this will be discussed in a later article dealing with forest).

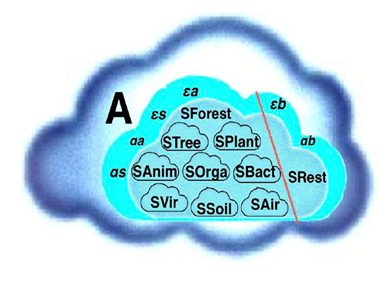
Now let's start with the brainstorming. We count first all subsystems of the forest, assigned as SSForest - the trees STree, where we include all bushes to get a better cut for the subsystem STree (the differences between trees and bushes are taxonomically not always clear) - the other plants which are not trees as SPlant - the animals, which live their life in the wood as SAnim - single cell organisms SOrga, which do not belong to either plants or animals - bacteria SBact - viruses and phages SVir - last but not least the inorganic part of the soil SSoil and the surrounding air and gases SAir - for something we might have missed, SRest.

We made it simple to define the cut but this does not mean we should not consider the interactions to the Allsystem A. Let's form classes to easier keep track of all interactions. The first are the interactions to the two main compartments of the wood. Inside the ground (soil) we call εs, αs and outside the ground (in the air) εa, αa. While there are interactions εb, αb, which interact with both parts of the wood, the air and the soil compartment. Light, or in general electromagnetic waves, for example acts upon the plants and heats up the soil. Or human visitors walking through the wood influencing the air part (fleeing animals, etc.) or as well as the soil part (soil compaction, etc.).

On the other hand we have material exchange between the All-System A and the wood leaving elements Sl or entering once Se. All of these with its interactions might have a big influence to the biocoenosis. The tree orchids in the Brazilian rainforest for example get their minerals from soil parts of the Sahara brought by intercontinental airflow.

Last but not least, we have the class of interactions αr, which we do not know or did not consider. The inner interactions in the System forest, SForest and between its subsystems will be discussed in a separate article, where we describe and model, SForest in more detail. The following picture summarizes symbolically the situation (figure 7).

At this point I will leave the examples, to go on with it, would fill chapters, which I will describe at a later stage, if we have learned more about the formalisms and techniques of modeling complex systems in a contextual system theory several real systems will be described in a following series of articles handling complexity.

Figure 7: Principal descriptive representation after a first brainstorming

Conclusion

As one might have noticed, the described definitions above are very close to the definition and strategy of object oriented programming like in Smalltalk or Java. I did this on purpose as it is the way to transfer the descriptive model almost directly into an object oriented program surrounding for modeling the complex system behavior embedded in its context. So a forest with its very high complexity and its even more complex context, can almost intuitively be formed into a computer model representing the thoughts combined with the scientific results and different mathematical descriptions. Using the modern tools of artificial Intelligence enables us to model high complexity by applying the iterative learning as an approach for getting answers in a complex world. In the future a formalism of symbolic representation of complex systems based on the described definitions should be developed helping us to ease understanding complexity. Using all the tools including mathematization, plausibility and the consequences of our intuitive view to complexity can be proven. Inconsistency will easily show up and by expanding the model into the future even small deviation to the reality will teach us where our thinking is wrong or fits the reality. This way leads to new research and experiments, clarifying our view, enabling us more and more to think about complexity and to leave the linear world.

Aside of this more intuitive formulation, it is important to integrate existing scientific laws and models into the description of complex systems. In a later article I will describe how several mathematical formulations, like matrix algorithm, operator formalisms or graphic calculations can be enclosed into the descriptive part. Transformation techniques like Fourier transformation, Recurrence plots, Phase space representations etc. help us to visualize special aspects in complex systems. It is important, that the state of the art in mathematics and science is always part of our view to complexity. Only obeying all the knowledge about the analyzed systems will bring us closer to the insight into the whole context and one can overcome the restricted view of a single science. This is of especially high relevance if we look at natural systems or human beings. The findings of Biophysics, Biochemistry, Molecular Biology, Evolution, Psychology, Sociology, Medicine and many more sciences have to be brought together, to get a reasonable view of our species. These will be the main topics of the following articles.

Reference

1. Nicolas G and Prigogine I. Preface in Exploring Complexity, W.H. Freeman and Company, New York, USA (1989).
2. Heisenberg,W. Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik, Zeitschrift für Physik 43 (1927): 172-198.
3. Lorenz E N. Deterministic Nonperiodic Flow, Journal of the Atmospheric Sciences 20 (1963): 130-141.
4. Lorenz E N. Predictability: Does the flap of a butterfly's wings in Brazil set off a tornado in Texas?, Title of the talk 1972 during the yearly meeting of the “American Association for the Advancement of Science” (1972).
5. R.P. Feynman, Phys. Rev 749 (1949).